Système de départage des exæquo dans le vote par jugement majoritaire

et infrastructure logique permettant la sélection de n'importe quel système de départage.

Résumé

Le vote par jugement majoritaire consiste à donner des notes à des candidats, et le scrutin de Condorcet consiste à les lister selon un ordre de préférence, ce qui est sensiblement la même opération, sauf que le nombre de mentions dépend du nombre de candidats et qu'une seule mention peut être attribuée à chacun d'entre eux. Le mode de calcul est lui aussi différent, mais on ne l'abordera pas ici. En pratique le scrutin de Condorcet ne permet pas de mettre à égalité ou de rejeter simultanément plusieurs ou tous les candidats. Et en pratique le vote par jugement majoritaire n'autorise pas à ne pas noter un candidat alors qu'on ne le connaît pas, mais cet écueil peut être autorisé si on admet qu'un non-vote revient à un vote pour la plus mauvaise note.

Ces deux systèmes de vote sont disponibles sur logic.ovh :  JM et  SC.
Cet article traitant des options de départage des exæquo, une page est dédiée à faire des tests :  logic.ovh

Introduction

Le vote par jugement majoritaire reste l'option la plus crédible aujourd'hui pour les référendum populaires. Sans revenir sur les avantages et inconvénients de chacun des systèmes de vote, les deux seuls systèmes valables sont le vote par jugement majoritaire et le scrutin de Condorcet. Le système de vote par jugement majoritaire étant plus commode pour l'utilisateur et plus facile sur le plan logiciel, nous focalisons plutôt sur lui.

En préambule il faut expliquer pourquoi. Le vote est une opération de l'indécidable, c'est à dire qu'en admettant l'absence de critères objectifs pour rationaliser un choix (du moins pour un référendum on s'imagine que ces critères sont antérieurs au seul fait de pouvoir se présenter), il s'agit de commettre une décision arbitraire.

Le choix du système de vote permet de minimiser l'arbitraire de cette décision. Ce qu'on désire, selon le critère de Condorcet, est que la solution, ou la personne élue, soit celle qui contente le plus d'électeurs. On pourrait étendre cette définition au fait de contenter le plus de monde, y compris les non-électeurs, chaque électeur se donnant la responsabilité de voter pour eux, mais bon.

Le scrutin majoritaire simple à deux tours est idéal dans un monde dépourvu d'informatique, où il s'agit de rédiger son choix sur un bulletin qui sera ensuite dépouillé, mais la solution obtenue au final ne crée jamais d'unanimité. C'est à dire qu'il existe d'autres candidats qui auraient été élus avec un autre système de vote, et qui auraient été plus appréciés.

Le vote par jugement majoritaire recueille plus d'information, ce qui lui confère un caractère qualitatif. Cela lui permet, moyennant un calcul des médianes, d'obtenir une vision plus précise de ce qu'on nomme la détermination publique. (Quand un pays est autodéterminé, on estime que la détermination publique peut s'exprimer librement et efficacement).

Le vote par jugement majoritaire (JM) possède une qualité indéniable et précieuse, qui consiste à transposer une évaluation subjective en une suite ordonnée objective. Cette transposition est d'une grande importance à faire noter, puisque l'intérêt des mathématiques consiste précisément à relater la réalité, et pour ce faire on élabore des mécanismes, dont on peut estimer le degrés de fiabilité.

En science on observe souvent que passer d'un champ à autre ne se fait jamais sans approximation. Par exemple quand une paille entre dans un verre d'eau (à la grenadine), le référentiel est modifié, la paille est "tordue". Quand on évalue la vitesse et la position d'une particule sous-atomique, le degrés d'incertitude d'une des deux valeurs dépend du degrés de certitude de l'autre. De même, lorsqu'on passe du subjectif à l'objectif, le résultat dépend de l'objectivité ou de la subjectivité du système de quantification de la réalité.

Les deux système de quantification de la réalité sont les mathématiques et la philosophie, et selon qu'on tende vers l'un ou l'autre, le système peut être aussi bien stupidement rigoriste que "idéologiquement déconnecté de la réalité" (ce qui revient un peu à la même chose...).

Ainsi le contre-exemple du système stupidement rigoriste qu'est le vote majoritaire à deux tours, est la vote par tirage au sort. Les arguments rationnels et objectifs contre ce principe sont évidents et inéluctables : on ne peut pas confier le destin d'un pays à un Donald Duck, incompétent, irrationnel, colérique, etc. (ce qui ne empêche pas que cela arrive). Mais sur le plan philosophique la valeur d'un tel vote a ceci de remarquable qu'une fois son mandat terminé, l'ancien élu retournera à la vie civile, où il devra faire face aux conséquences de ses actes... ce qui n'est pas le cas des hommes de pouvoir en général.

La nature du poste à pouvoir suite à un choix indécidable est donc complètement modulé par le système de vote, poussé à l'extrême sur la borne philosophique dans le cas du tirage au sort, puisqu'il perd sa dimension autoritaire et représentative, paternaliste, pour ne garder que sa dimension fonctionnelle, qui est l'accomplissement d'un travail concret. Il est donc prévisible qu'un élu par vote aléatoire développe son sens de la citoyenneté, qu'il ait une meilleure écoute des besoins, et diminue grandement l'espace entre les hiérarchies, ce qui se répercute dans toute la société, où les relations sont dès lors plus harmonieuses. Donc sur le plan philosophique, c'est très valable.

La vote par jugement majoritaire se situe entre ces deux bornes. C'est un système concret qui quantifie l'opinion publique pour en faire une cartographie, dont on essaie de tirer le meilleur compromis. La conséquence mathématique est que cela ne peut se faire sans informatique, ni de façon distribuée, mais seulement centralisée. C'est la raison pour laquelle Condorcet jugeait que son système de vote, s'il était évidemment meilleur, était infaisable il y a trois-cent ans. Il devait dire cela avec beaucoup de regrets, mais forcé par l'objectivité. Mais heureusement on a inventé l'informatique.

Sur le plan philosophique, on ne peut que spéculer, mais au moins il est certain que face à la preuve quasi-scientifique que l'élu est le meilleur choix, les électeurs battus auront une meilleure compréhension et acceptation de ce choix, ce qui aura pour effet de faire diminuer les polarisations politiques.

Les incertitudes du système de vote par jugement majoritaire

L'écriture d'un algorithme pour déterminer le résultat d'un vote par jugement majoritaire n'est pas aussi évident que le laisse croire la simple lecture de l'énoncé de la procédure. Elle permet d'expérimenter les incertitudes du résultat.

En définitive le logiciel que nous construisons n'est rien d'autre qu'une fonction d'assortiment des valeurs, de la même manière que la fonction sort() permet d'ordonner des nombres. Cela peut se comparer aussi à un diagramme de Hasse, qui montre les différentes manières d'ordonner les nombres binaires de 0000 à 1111. Tout l'enjeu du système de calcul va consister à ordonner des résultats dans un sens qui semblera naturel si on tient compte de tous les éléments. Il est très probable qu'un résultat n'affiche pas un assortiment des candidats qui paraisse satisfaisant. Et à cela il y a plusieurs raisons, outre une fausse impression.

Pour minimiser (rendre nulles) les incertitudes liées à la conception du logiciel en lui-même, il s'est agit pour nous de différencier deux zones de calcul distincts, celle qui est purement procédurale et celle où se joue l'algorithme de départage des égalités. Car quand on écrit le logiciel on est naturellement amenés à faire tout en même temps. Mais ce n'est qu'un échafaudage pour construire ensuite une jolie application.

Originellement le départage des égalités n'a de raison d'être que pour isoler le gagnant de l'élection, et on laisse les autres résultats dans la corbeille, en se moquant de savoir s'ils sont bien ordonnés. Mais ce n'est pas ce que nous voulons. Le système de vote par jugement majoritaire est si intelligent et pertinent qu'on lui réserve de nombreux autres usages, voire même d'en faire une routine automatique de processus plus complexes.

Pour cette raison, une composante essentielle pour nous est la vitesse d'exécution de l'algorithme. De même, pour un scrutin portant sur des millions de votes, il est certain qu'il va falloir une machine très puissante pour en venir à bout, en particulier en utilisant la méthode de départage originelle. (Et on ne parle pas de celle de Condorcet).

Avec le système de départage originel de Balinski et Laraki, qui consiste à itérer les votes, cent-mille votes sur huit propositions prend dix secondes, tandis qu'avec le système de départage par groupe d'insatisfaits d'Adrien Fabre, qui consiste à itérer les mentions, le même calcul prend un millième de seconde, soit dix-mille fois moins de temps. Un million de votes sature les huit gigas de RAM de notre serveur, avec la méthode 1.

La méthode de départage 1 (D1) offre des résultats plus précis et un meilleur ordonnancement des résultats, avec moins d'exæquo. La D2 est la moins mauvaise des solutions pour l'instant, bien qu'on ne se privera pas d'en essayer d'autres. Elle offre des résultats presque identiques à la première méthode, et même de meilleurs quand il y a peu de candidats et de votants.

Exemples d'un résultat avec D1 :

Résultat du même vote avec D2 :

Pour vous, qu'est-ce qui est le plus juste ?

En acceptant la notion d'égalité indiscernable par le calcul, on s'autorise un ordonnancement faisant usage du hasard. Ainsi le système de vote tend vers une solution philosophique. Du coup il faut parler de vote par jugement majoritaire randomisé.

Les égalités deviennent un sujet complexe lorsqu'on veut ordonner une liste

Dans le second cas que nous présentons, il a fallu procéder à un tirage au sort des égalités indiscernables entre les candidats "c" et "f". Avec le premier système de calcul, il n'y a aucune incertitude sur le résultat. On peut simplement se demander (dans la figure 1) s'il ne serait pas plus "juste" que le candidat "h" soit monté d'un rang à la place du candidat "g". L'algorithme D2 a pu faire cette opération.

Durant le calcul, il arrive souvent que les égalités soient multiples, et même qu'il y ait différents groupes d'égalités, formant des blocs dont on sait d'avance comment ils seront ordonnés.

Cette mécanique d'ordonnancement des groupes d'égalités avant-même de procéder à leur calcul se produit dans ce que nous nommons l'infrastructure logicielle. Elle est élémentaire et ne provoque aucune erreur. Elle peut être écrite de différentes manières mais nous avons préféré celle qui est la plus courte, et limpide à condition d'en saisir les principes.

Il est presque inutile de dire que dans sa première version de l'algorithme, figée avec la première méthode de départage, le code était confus, redondant selon diverses méthodes, et assez lent à exécuter. La solution que nous proposons ici est généralisable à toute application désirant procéder à un dégrossissement des résultats par passes successifs.

Les deux méthodes de départage D1 et D2 nécessitent une itération pour être accomplies. La méthode D2 peut aussi bien trouver un résultat à la première itération qu'à la [demi-nombre de mentions moins le modulo de 2 du nombre de mentions] itération (s'il y a cinq mentions, à la deuxième itération).

Lorsqu'une tri-égalité est rencontrée, l'algorithme va chercher à isoler un candidat unique qui se détache par le haut des autres candidats. Le meilleur supporter ou le meilleur opposant. Celui qui a le meilleure score est rangé dans le caddie. Mais aucun traitement n'est prévu pour discerner celui qui se détache par le bas, lorsque les deux autres lui sont supérieures et à égalité. Dans ces cas, une fois l'élément détaché, les égalités restantes sont renvoyées à la moulinette, en la recommençant à zéro.

Les autres groupes d'égalités qui viennent après seront traités de la même manière, selon la routine habituelle d'itérations séquentielles (comme les balises html, qui son imbriquées mais aussi consécutives).

Système de parcours de groupes successifs imbriqués

Pour concevoir cet algorithme, il faut avoir les idées claires et pouvoir dessiner les processus. Car s'il est certain, d'après la correspondance Curry-Howard, que tout algorithme correspond à une démonstration mathématique, il vaut mieux cependant veiller à ce que cet algorithme reste compréhensible et schématique, de façon à en appréhender la logique.

Il s'agit d'une itération en spirale, qui se joue entre trois seules fonctions, qui sont appelées à partir du moment où des exæquo ont été détectés.

L'essentiel du calcul originel des médianes est laissé en amont, tandis que le système de départage (tie-break) reste optionnel. De cette manière nous pouvons sélectionner n'importe quel système de départage et en tester de nouveaux.

L'algorithme infrastructurel est très simple, c'est pourquoi nous le publions ici, en espérant qu'il serve de modèle pour ce genre de cas de figure.

Le principe d'une itération en spirale est de se réserver différents chemins itératifs allant de plus petit au plus grand.

L'itération spirale (utilisée dans les systèmes de départage des groupes successifs d'égalités potentiellement imbriquées)

Pour suivre les étapes du calcul nous avons placé des témoins à la fin de chaque fonction, qui relatent l'état des données à la sortie et des indications sur ce qui s'y est passé.

La fonction de résolution succède à la fonction solution(), qui produit un schéma de travail.

La fonction de solution est nourrie par les résultats du calcul des médianes pour chaque candidat. Elle produit les données attendues par la fonction de rangement rank(), qui va produire une liste ordonnée de candidats, auxquels il n'y a plus qu'à associer une représentation graphique.

La variable qui va être construite par le processus resolution() est donc de même format que la variable produite par la solution. Optionnellement aucune résolution peut n'avoir à être accomplie. Ce schéma de travail (la variable produite) consiste en un tableau imbriqué qui signifie que lorsque deux valeurs sont dans un même tableau, alors elles sont à départager. C'est idiot car toute valeur est dans un tableau. Mais cela dépend d'où se place le curseur de l'exécution du code : lorsqu'il est dans une itération, les itérations précédentes sont figées et uniques.

Il n'y a aucun doute qu'à la fin du calcul de la résolution, le tableau généré peut posséder un grand nombre de dimensions. Elles seront aplaties par la fonction rank(), étant donné qu'on aura prit soin de remplir la variable $rk dans l'ordre résultats obtenus, même s'il est différent de l'ordre des inégalités résolues (on peut déterminer "un dernier de la liste" et écrire ensuite ceux qui précèdent).

Le format de la variable $rk est donc de complexité minimale. En sortie de solution, elle peut ressembler à ceci (pour le test présenté) :

[solution] => [0 => [0 => 7, 1 => 1, 2 => 8], 1 => [0 => 2, 1 => 3, 2 => 4, 3 => 6]] 2 => 5

Dans cette variable on voit que les candidats sont classés en deux groupes d'égalités, qui devront être élucidés, mais dont on sait au moins comment ils sont ordonnés. Le dernier résultat est unique, sa place ne sera pas impactée par le calcul.

En effet la fonction de résolution consiste seulement à ranger les candidats uniques dans la variable $rd, qui sera greffée à n'importe quel endroit de $rk, et à envoyer les égalités vers resolve(). Cette fonction est appelée une première fois par la mesure d'exæquo, puis autant de fois que nécessaire lors d'une sous-routine de resolve(), quand notamment le calcul a trouvé des certitudes et des incertitudes, qui elles devront repartir pour un tour, tandis que les certitudes seront classifiées et figées.

La fonction resolution() :

La fonction resolve() :

On va les détailler.

Les variables $a,$rb,$rm,$rt,$m sont transportées tout du long du processus, à toutes fins utiles. Seule la variable $r, le tableau-maître qui contient l'intégralité des votes, est laissé dans une variable de classe. Elle n'est utile que pour le système de départage D1.

• $a désigne l'application qui sera utilisée pour le départage.
• $rb désigne la solution retenue. Elle deviendra $rd en sortie de resolve(), et rk en sortie de resolution(). Elle consiste à mettre les clefs des candidats en tant que valeurs d'un tableau multidimensionnel ordonné.
• $rm est le tableau des mentions majoritaires pour chaque candidat.
• $m est un paramètre qui sera utile par la suite pour tester différentes solutions de départage. Il fixe le milieu de la médiane à 0,5.
• $n est le numéro de l'itération de resoltion().
• $o est le numéro de l'itération de resolve().
• $u sera le numéro de l'itération de la fonction de départage tiebreak1().
• La variable de classe $rf collecte les activités pour pouvoir suivre le déroulement du calcul.

La fonction resolution() est très élémentaire, elle passe en revue $rb et envoie au charbon les égalités signalées par des tableaux.

La fonction resolve() a pour rôle de discriminer les résultats certains des résultats incertains, et peut faire appel à la fonction tiebreak() aussi bien qu'à la fonction resolution() pour une seconde itération de celle-ci. Elle permet également de fixer les incertitudes indécidables par une randomisation des résultats, ce qui permet de résoudre le calcul arbitrairement. Une contention des explosions est prévu, outre celle qui est propre à la méthode D1 qui limite les itérations à un seuil proche de la ruptures de ressources. On limite seulement à dix itérations de resolution() la recherche de groupes d'égalités, maximum pour un scrutin à cent candidats.

Cela peut paraître contre-intuitif que cette fonction ne soit pas chargée de la résolution du problème promise par la fonction précédente. Elle ne fait que traiter les résultats obtenus par la fonction de départage, appelée dès l'entrée. De plus elle débute par l'assortiment des données reçues, alors qu'elle étaient déjà ordonnées par solution(), et considérées comme égales.

La fonction qu'on peut voir countr() consiste en un équivalent de la fonction native array_count_values(), mais applicable à des valeurs à virgule flottante. Elle permet de détecter les résultats identiques, comme le fait solution().

Finalement la fonction resolve() est elle aussi très simple, elle fait appel à la fonction suivante et à la précédente, détermine un tirage au sort, renvoie les données traitées à son prédécesseur, et ne commet aucune opération sur les données. En quatre lignes. Ces deux fonctions n'ont qu'un rôle structurel. Cette structure permet d'envoyer itérativement le traitement de toutes les égalités et sous-égalités découvertes. Elle est très élémentaire.

Cette méthode algorithmique a aussi l'avantage de clarifier les idées du grand public, toujours inquiets de ne pas savoir ce qu'il y a dedans. L'avènement du système de vote par jugement majoritaire va un peu de pair avec un minimum d'éducation informatique.

Les fonctions de départage

La méthode D1 (itération des votes)

La fonction originelle D1 est très simple, elle consiste en une boucle qui retire le dernier vote de la mention obtenue et recalcule la nouvelle mention majoritaire dans ce cas. Il est même inutile d'appeler la fonction sur elle-même, puisque tout se passe dans une boucle while(). Cette boucle s'arrête dès que le tableau des mentions $rm affiche des résultats inégaux, que rend visible un array_count_values().

La méthode D2 (itération des mentions)

La fonction des groupes d'insatisfaits est dite calculatoire, là où la première est procédurale. Elle est des milliers de fois moins gourmande en ressources, puisqu'elle consiste à comparer le pourcentage de votes obtenus pour le cumul de toutes les mentions avant et après la mention majoritaire. Sur cinq mentions, il n'y a que deux à quatre itérations possibles. Le curseur compare les meilleurs scores d'opposants et de supporters, et en cas d'égalité à la fin de la boucle, il choisit arbitrairement de tenir compte des opposants.

La fait d'ajouter la procédure qui consiste à délibérer en cas d'impossibilité de le faire, que le perdant sera celui qui a le plus d'opposants, est un peu litigieux. C'est justement ce qu'on cherche à définir, en faisant un savant calcul, mais là on décide de le résoudre en ne tenant compte que de la mention "à rejeter", c'est à dire qu'on donne raison aux opposants. Procéder de la sorte oblige à faire que la plus basse mention signifie bien "à rejeter" et aucune autre chose. C'est grâce à cette mention, et à la procédure qui lui est associée, qu'on peut se permettre de laisser le votant libre de ne pas voter pour tous les candidats, ce qui revient au même que de leur attribuer la plus mauvaise mention. En d'autres cas, l'oubli d'une mention aussi bien que la délibération forcée devraient être interdits.

En principe, le JM autant que le SC n'ont que faire de la quantité de votes, seulement de leur qualité. Mais la quantité peut être une données intéressante, mais au risque de créer plus d'incertitudes dans les résultats si on en tenait compte. Se débarrasser de la quantité des votes allège providentiellement l'efficacité du calcul du résultat, c'est pourquoi en principe toutes les mentions doivent être votées. La quantité de vote est une autre question que le vote, mais peut vite devenir significatif à un autre niveau.

L'avantage de la méthode D2 est sa rapidité, et son inconvénient est son imprécision. Beaucoup plus d'exæquo sont trouvés. Ce n'est donc pas une méthode idéale pour intégrer un tel système d'ordonnancement dans au sein d'un processus plus global qui y ferait appel de manière fréquente. Il n'est pas vraiment prévu pour s'occuper de classer correctement les autres candidats que le vainqueur. Cependant elle offre des résultats très comparables à la première méthode, et parfois ils sont intuitivement meilleurs.

Cette méthode peut être utilisée pour les petits et gros scrutins, tandis que pour les petits et moyens scrutins avec beaucoup de candidats, on préférera utiliser la méthode D1. On sera tenté, en cas d'incertitude du résultat, d'aller vérifier le calcul avec la méthode D1.

Quand il arrive que le meilleur score pour une mention soit égal à celui d'autres candidats. Dans ce cas on place ces égaux dans un même groupe d'égalités, qui devra être départagé (sans l'interférence des autres), tandis que les candidats suivants seront renvoyés à une nouvelle itération de départage (la fonction du bas qui recommence tout à zéro).

Il est regrettable que la règle ne soit pas émise de certifier qu'en cas d'égalité du meilleur score, les candidats restants sont "naturellement" classés après les premiers. Mais pour la construction du logiciel on a bien été obligés de le délibérer. Sinon cela consisterait à renvoyer une triple-égalité dans une itération idempotente.

Pour la construction de cet algorithme, on décide d'affecter un système de scores aux résultats, borné de 0 à 100, en décrémentant les bornes maximales et minimales à chaque itération, et en laissant les scores intermédiaires "au milieu". De cette manière le plus bas score d'une deuxième itération est un plus haut score que le plus bas score de la première itération. Mais ceci n'est qu'une option technique. Toute idée est la bienvenue. Dans la version d'échafaudage, ce problème était réglé "naturellement" en plaçant les derniers dans une variable prise en compte seulement à la fin du processus. Mais quoi qu'il arrive la règle de départage est pleinement respectée.

Pour rire, voici le déroulement du script pour les exemples donnés :

[1] => Array ([tiebreak2.1.0.2] => Array (=> looser: 7 [opponents/supporters] => Array (
[8] => Array (=> 0 [1] => 0)
[7] => Array (=> 0.1 [1] => 0))
[given notes] => Array ([8] => 3 [7] => 2)))
[2] => Array ([tiebreak2.1.0.1] => Array (=> ex aequo [opponents/supporters] => Array (
[8] => Array (=> 0.2 [1] => 0)
[7] => Array (=> 0.2 [1] => 0))
[given notes] => Array ([8] => 3 [7] => 2)))
[3] => Array ([tiebreak2.1.0.0] => Array (=> ex aequo [opponents/supporters] => Array (
[8] => Array (=> 0.3 [1] => 0.4)
[7] => Array (=> 0.2 [1] => 0.4))
[given notes] => Array ([8] => 3 [7] => 2)))

Le déroulement se lit de bas en haut, nous sommes dans la unième itération globale (après la zéroième), il s'agit de départager les candidats 8 et 7, à gauche les opposants et à droite les supporters, le meilleur score gagne, et il faut attendre la troisième sous-itération pour déterminer un perdant certain (le candidat 7).

*

D'autres méthodes ont été ajoutées pour le plaisir de faire des tests, qui sont souvent moins concluants que les méthodes D1 et D2, et parfois non.

La première méthode alternative que nous présentons (D3) est une candidate pour devenir une méthode officielle.

La méthode D3 (Médiane flottante)

La méthode D3 est très amusante, elle consiste à départager des exæquo en déplaçant le centre de gravité de la médiane, qui est "naturellement" "au milieu" des votes. La médiane détermine le score obtenu au moment où il y a autant de votants après qu'avant. Mais si on pose cette question à 60% du parcours, on aura peut-être une possibilité de faire un départage. C'est une autre méthode de la meilleure médianerl qu'on pourrait appeler "de la médiane flottante".

Le curseur va tester itérativement, en spirale, les médianes autour de 0.5 : 0.6, 0.4, 0.7, 0.3, etc.

Le résultat obtenu est assez probant. Il offre parfois des arrangements plus recevables qu'avec les autres méthodes. Il est aussi rapide que la méthode D2. Il présente beaucoup moins d'exæquo. Ses résultats sont plus proches de la méthode D1. Cela nous semble un excellent candidat, qu'on va s'empresser de tester sous toutes ses coutures.

Les résultats produits sont exactement ceux de la méthode originelle D1, il n'y a aucun exæquo, et la vitesse d'exécution est la même qu'avec la méthode D2.

Sur les votes avec un plus grand nombre de votants (dix candidats et cent votants), cet algorithme produit plus de groupes d'incertitudes qu'avec les modèles D2 et D1, qui en produit le moins. La méthode D2 produit moins de groupes d'incertitudes mais chacun contient un d'autant plus grand n'ombre d'exæquo, ce qui rend ma méthode D3 plus précise (moins incertaine).

La méthode D4 (pourcentages)

Une première méthode (après celles qui sont officielles) ultra simple consiste seulement à répondre à une question primitive : pourquoi, au lieu des meilleures mentions, ne tient-on pas compte des pourcentages de votants ayant permis d'atteindre cette mention majoritaire ? D'autant plus que cela aurait pu être fait dès le début du calcul. Mais c'est une question-piège. Ce qui fait la pertinence du vote par jugement majoritaire est qu'il construit une règle telle que le votant n'a pas besoin de tricher dans l'énoncé de son "jugement". Au contraire, plus il sera honnête, plus le résultat sera fiable. La triche est une chose fréquente et presque instinctive, dès lors qu'on est confrontés à des systèmes imparfaits.

Le système ne serait plus indépendant aux alternatives non-pertinentesrl si on en confiait la procédure à la stricte scorification, car cela inciterait les votants à polariser leurs votes. Or, s'ils se contentent des mentions extrêmes pour chaque candidat, cela revient très exactement à la même chose qu'un vote majoritaire simple.

La méthode D3 donne seulement un état des lieux sur (ce qu'on appelle) la scorification. Elle produit beaucoup d'ex-æquo.

La méthode D5 (Chips)

La méthode D5 répond à une autre hypothèse, elle aussi intuitive : que se passerait-il si on accordait à chaque mention un coefficient de pondération, de telle sorte que chaque mention ait une valeur attitrée ? C'est la méthode des "Chips", où on affecte des jetons à chaque mention, comme des pièces et des billets. Mais dans ce cas encore, on ne fait que "mathématiser" un processus conçu pour rester un minimum philosophique. On s'est aussi amusés à multiplier ou mettre au carré les scores, sans trop de succès, quoi cela soit intéressant.

La méthode D6 (Averages of medians)

L'enjeu qui paraît devoir être atteint est de pouvoir classifier les candidats selon un ordre que l'intuition peut accepter sans trop de doute. Il arrive quelquefois que cela ne soit pas le cas. Quand un problème de ce type tombe sur un maniaque du rangement, il ne peut que susciter une nouvelle vocation. Intuitivement on a envie que les basses notes aillent en s'accroissant et les hautes, en décroissant, au fur et à mesure du classement. C'est le cas dans une demi-mesure pour les mentions proches du bord, tandis que la mention du milieu peut indifféremment être classée comme elle veut.

Cette idée est à la base de la méthode D6, qui cherche à faire des moyennes à partir des scores des médianes. On l'appelle la méthode des moyennes de médianes. Elle est en cours de développement.

La méthode D7(Growth speed)

Une méthode D7 consiste à faire une course à la mention, où on calcule la différence de retard ou de l'avance d'un candidat lorsque le curseur va de la plus mauvais à la meilleure mention. En principe ils arrivent en même temps sur la ligne d'arrivée, mais la vitesse diffère selon les mentions. Ce système serait intéressant sur un vote qui porte sur une centaine de mentions. Cette méthode n'est pas encore développée.

L'application de tests

Une application a été développée pour faire des tests, et elle est disponible pour le public sur la page de l'app  logic.ovh.

On peut y tester différentes méthodes avec un même jeu de données, on peut générer des jeux de données en spécifiant le nombre de mentions, le nombre de candidats et le nombre de votants, et suivre le processus calculatoire (option verbose).

Les données utilisées pour l'exemple de ce document sont celles-ci :

2,1,2,2,3
3,2,2,1,2
1,3,2,2,2
1,2,3,1,3
2,4,2,0,2
1,2,3,2,2
1,1,0,4,4
0,2,1,3,4

Les colonnes fournissent le nombre de votants pour chaque mention, et les lignes sont les candidats.

Autres tests avec la méthode à médiane flottante

Devant le vif intérêt de cette nouvelle méthode de départage, nous cherchons à approfondir ses avantages et inconvénients.

Parmi les sources de données, le bouton "judment" renvoie les données collectées par l'App du même nom. Les jeux dont les ID sont 11 et 6 nous intéressent.

Test ID11

L'ID 11 est un vote sur quatre candidats faisant intervenir neuf votants. Il est intéressant parce que la méthode D2 produit un résultat qui semble intuitivement meilleur que la méthode D1, tandis que la D3 est identique.

D1 : Le gagnant est : a avec mention: 3 Supporters : 55.56% Parmi 9 votants

D2 : Le gagnant est : b avec mention: 3 Supporters : 77.78% Parmi 9 votants

D3 : Le gagnant est : a avec mention: 3 Supporters : 55.56% Parmi 9 votants

Test ID 6

Le test avec l'ID 6 permet de voir que là encore, la méthode D3 produit les mêmes résultats que la méthode D1, et qu'il y a moins d'exæquo, répartis dans plus de groupes d'égalités (ce qui est mieux).

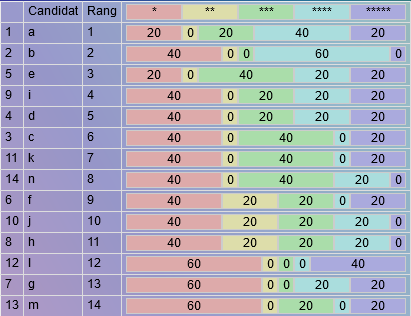
D1 : Le gagnant est : a avec mention: 2 Supporters : 80% tirage au sort entre d i ; tirage au sort entre c k ; tirage au sort entre j h ; Parmi 5 votants

D2 : Le gagnant est : a avec mention: 2 Supporters : 80% tirage au sort entre e d c k i n ; tirage au sort entre j h ; Parmi 5 votants

D3 : Le gagnant est : a avec mention: 2 Supporters : 80% tirage au sort entre d i ; tirage au sort entre c k ; tirage au sort entre j h ; Parmi 5 votants

Test minimal

Le test présenté dans Wikipediarl pour démontrer la méthode D2 permet de visualiser un exemple de résultat "plus intuitif" que celui obtenu par la méthode D1. La méthode D3 produit le même résultat que la D1.

D1 : Le gagnant est : a avec mention: 4 Supporters : 83.33% Parmi 6 votants

D2 : Le gagnant est : a avec mention: 4 Supporters : 83.33% Parmi 6 votants

Tests avec d'autres finesses de résolution

Après de nombreux tests, on s'est aperçu qu'on pouvait tout aussi bien augmenter la résolution de l'algorithme en choisissant un pas de 0.01 point au lieu de 0.1. Dans ce cas les résultats obtenus sont très proches de ceux de la méthode D1. Avec un pas de 0.01, il faut au maximum cent itérations par mentions pour faire le tour des possibilités avant d'aboutir à une égalité (et dix avec un pas de 0.1), là où pour un vote massif la méthode D1 va nécessiter des millions d'itérations.

On peut ajouter un moyen d'adapter le pas au nombre de votes, sur la base de 10 candidats * 1000 votants nécessite un pas de 0.01 (soit 100/10*1000). Ce réglage ne produit que 10% d'incertitudes dans les tests randomisés. Quand des incertitudes apparaissent, il suffit d'augmenter le pas de la résolution (ce que le logiciel peut faire automatiquement, et uniquement dans les portions où cela est nécessaire, pour cela on a placé la méthode 3b).

Le fait de vouloir résoudre des calculs bien plus raidement n'est pas très utile pour un vote unique, mais peut devenir très important dans le cadre d'une routine chronique au sein d'un calcul plus vaste. Il est possible d'adapter automatiquement le pas pour adapter le nombre d'itérations aux besoins de chaque calcul.

En cas de nécessité d'économiser encore plus les ressources, on peut aussi demander à cette méthode tenir compte de la règle des groupes d'insatisfaits en cas d'égalité. On testera cela dans la méthode D3b, avec un pas de 0.1.

Enfin, on peut voir quelques variations entre la méthode D1 et D3 :

Le gagnant est : j avec mention: 3 Supporters : 62% Parmi 100 votants

Le gagnant est : c avec mention: 3 Supporters : 63% Parmi 100 votants
Le gagnant n'est pas le même, la méthode D3 semble privilégier les votes polarisés (sauf dans cet exemple) mais on est assez satisfaits des positions données ici aux candidats c et j, et au groupe i et j.

Dans le précédent résultat, la finesse est de 1/50, voici le résultat avec une finesse de 1/100 (une plus grande finesse ne change rien, et une finesse de 1/10 produit trois groupes d'incertitudes) :

On voit que c'est "mieux ordonné", entre f, i et b, et plus conforme à D1. Seul le gagnant a changé.

Ce que nous cherchons, "bien ordonner les lignes", nécessite encore une preuve que les lignes sont bien ordonnées. Mais le fait d'obtenir quasiment les mêmes résultats avec deux méthodes est plutôt encourageant. Du moins, contrairement à ce que dit la page wikipediarl, la méthode D2 n'est pas égale à la D1, mais la D3 est presque similaire.

Code de ce test :
26,17,16,18,23
15,18,25,22,20
14,23,15,26,22
22,17,23,20,18
19,21,18,22,20
23,17,16,17,27
19,26,14,22,19
25,21,18,18,18
19,19,19,21,22
24,14,14,26,22

Critiques du système de vote par jugement majoritaire

Dans les milieux où le public est appelé à contribution pour apporter des innovations politiques, comme les consultations populaires (Le jour d'Après, consultations sur le climat, Mouvement Constituant Populaire, etc.) le système de vote par jugement majoritaire est reçu avec froideur. Même les logiciels permettant de faire ces consultations comme Decidim ne l'utilisent malheureusement pas. Dans les milieux politiques, à moins d'être un challengeur qui cherche l'innovation et accepte de "tester éventuellement l'idée", le sujet semble clos. De même dans les associations, les votes se vont prioritairement à la majorité simple. C'est une grave erreur. Mais surtout les discussions pour engager le débat sont très rapidement écartées d'un revers de la main. L'argument est le suivant "le jugement majoritaire ne respecte pas le principe de Condorcet". Et ceci alors que tous les autres systèmes de vote le respectent encore moins.

Il peut sembler que ces milieux sont toujours habités par au moins une personne qui convainc les autres de ne pas suivre cette voie. Et il est évident que sur le plan politique cette méthode est rejetée avec vigueur pour des raisons stratégiques. La principale de ces raisons est que la polarisation voulue des électeurs simplifie les débats, et permet d'associer des critères subjectifs par grands paquets. De cette manière, quelle que soit le bord politique choisi, les objectifs des multinationales peuvent y être associés.

Les critiques objectives "plus scientifiques" qu'on peut trouver mettent en évidence le principe de l'électeur du diable, celui dont l'intervention à elle seule suffit à faire pencher le résultat vers un candidat qui n'est pas du tout celui de Condorcet. Mais si on regarde bien, ce cas de figure n'émerge que lorsque le nombre de mentions envisagées est de l'ordre de la vingtaine. Il est absurde de demander un vote sur vingt mentions. Les auteurs du Jugement majoritaire spécifient très clairement qu'il ne peut y avoir qu'entre cinq et sept mentions. De plus ils précisent qu'une question doit être explicitement posée, afin que le scrutin en soit la réponse. Dans les contre-exemples qui sont donnés, aucune question n'est posée.

En conclusion il n'y a pas de critique réellement objective du système de vote par jugement majoritaire. C'est un système qui requiert de l'informatique et correspond à ce que notre époque peut se permettre. Il est plus juste et plus rationnel. Il relate mieux la réalité. De plus nous avons montré une algorithmie enfantinement facile à comprendre, de façon à rendre les entrailles du logiciel plus claires pour le grand public.

Pour bien faire, les données des votes devraient être distribuées et être calculées en parallèle par diverses machines indépendantes. Du côté de la sécurité des votes en eux-mêmes, chacun doit pouvoir constater, ou faire constater par un réseau d'amis chargé de garder le secret du vote, que l'ID qui leur a été attribué correspond bien aux votes qu'ils prétendent avoir fait. Il n'y a donc aucun problème de sécurité tant que les données sont publiées en Open Data. On pourra même refaire des calcul en fonction des données vérifiées, oubliant celles qui ne le sont pas. Après tout, puisqu'il n'y a besoin que d'un tour pour l'élection, on peut aussi bien consacrer la deuxième aux validations.

De cette manière le scrutin seraient encore plus sécurisé que l'actuel scrutin par vote majoritaire sur papier libre, et dont la transparence ne repose que la confiance.

Conclusion

Pour les besoins de notre réseau social, nous utiliserons la méthode D3. En effet il est plus rapide à l'affichage de faire les calculs directement que de les appeler depuis une base de données. Mais lorsque des groupes d'égalités auront été détectés, nous laisserons l'option de demander un résultat "plus précis" en utilisant la méthode D1.

La méthode algorithmique que nous avons proposée est la plus grande minimisation possible du problème rencontré de départage des groupes successifs et imbriqués d'exæquo. Il est possible d'en faire une nouvelle méthode de fraction continue.

Enfin, la méthode de calcul via un graphe en réseau du scrutin de Condorcet reste à faire. Pour l'instant l'App Condorcet utilise la méthode calculatoire D3. Mais dans l'avenir le JM pourra optionnellement faire appel à la méthode de Condorcet, pourvu que son algorithmie la rende exploitable à grande échelle.

 telex.ovh